Error Code: EXCEPTION - Ungrounded Variable

This guide explains why an ungrounded variable error may occur and describes how to fix it.

In Rel, a variable is grounded when it can be instantiated to a specific, finite set of values.

For instance, in the expression x: range(1, 100, 1, x), the variable x is instantiated with the values 1, 2, ..., 100.

By contrast, a variable is not grounded or is ungrounded if the system is unable to determine a way to instantiate a finite set of values.

Example: Infinite Possibilities

For example, in x: minimum(1, x, 1), there are infinitely many values of x for which minimum(1, x, 1) is true. In fact, this is the case in many relations defined in Rel Libraries, such as in the example above with minimum.

Consider another example that returns an ungrounded variable error:

def my_string = substring["abcd", -2]
def output = my_string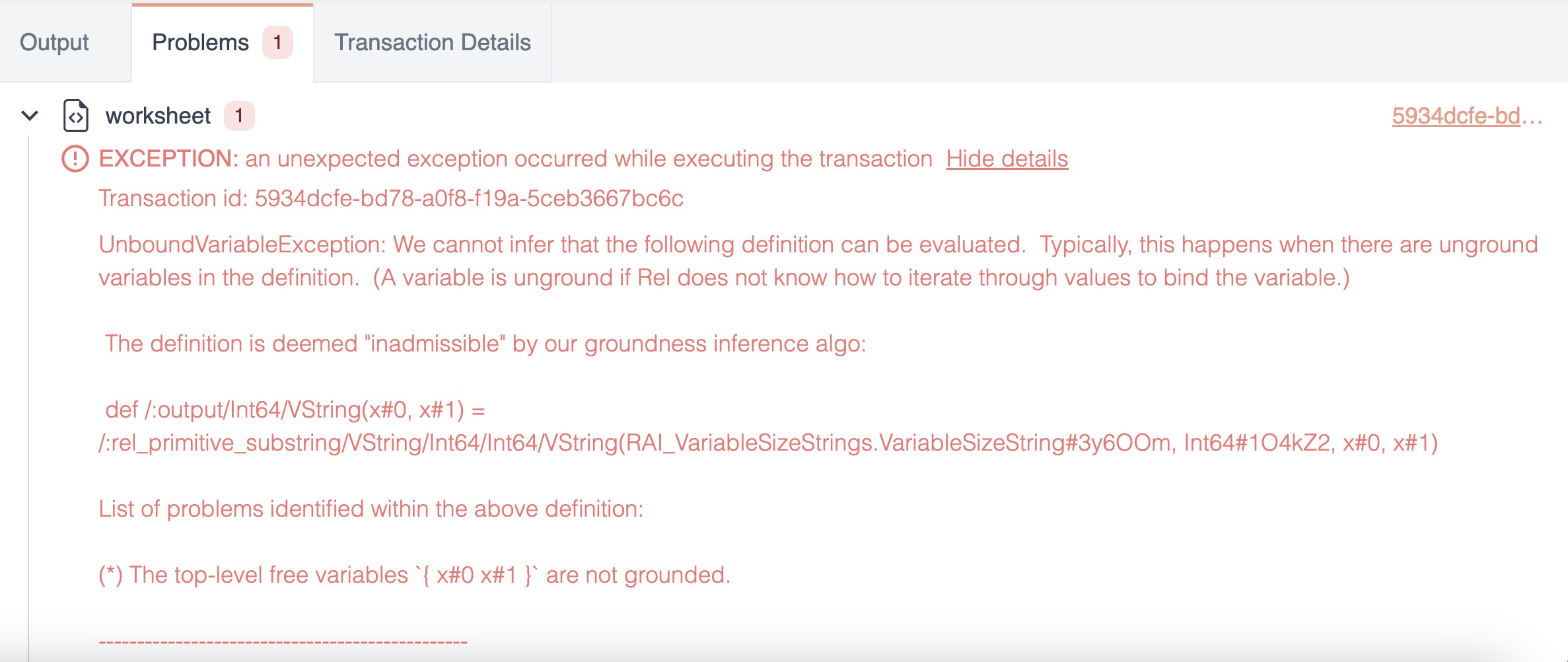

The example above defines the relation my_string as a substring of the "abcd" string, using the built-in substring relation. This returns an EXCEPTION error thrown by the query optimizer.

Because this third argument is allowed to be larger than the length of the string, the number of valid values is infinite. To fix this problem, you need to provide another argument to substring that states where the substring should end. For example, the substring could end after the second character:

// read query
 
def my_string = substring["abcd", -2, 2]
def output = my_string

Example: Nonlinear Dependencies

Another reason an ungrounded variable error can occur is when nonlinear mathematical dependencies need to be resolved. In general, no closed form solutions (opens in a new tab) exist for these nonlinear dependencies, making it impossible for the system to determine all valid values.

For example:

def output(x, y) {
    x = 4
    and y^2 = x
}

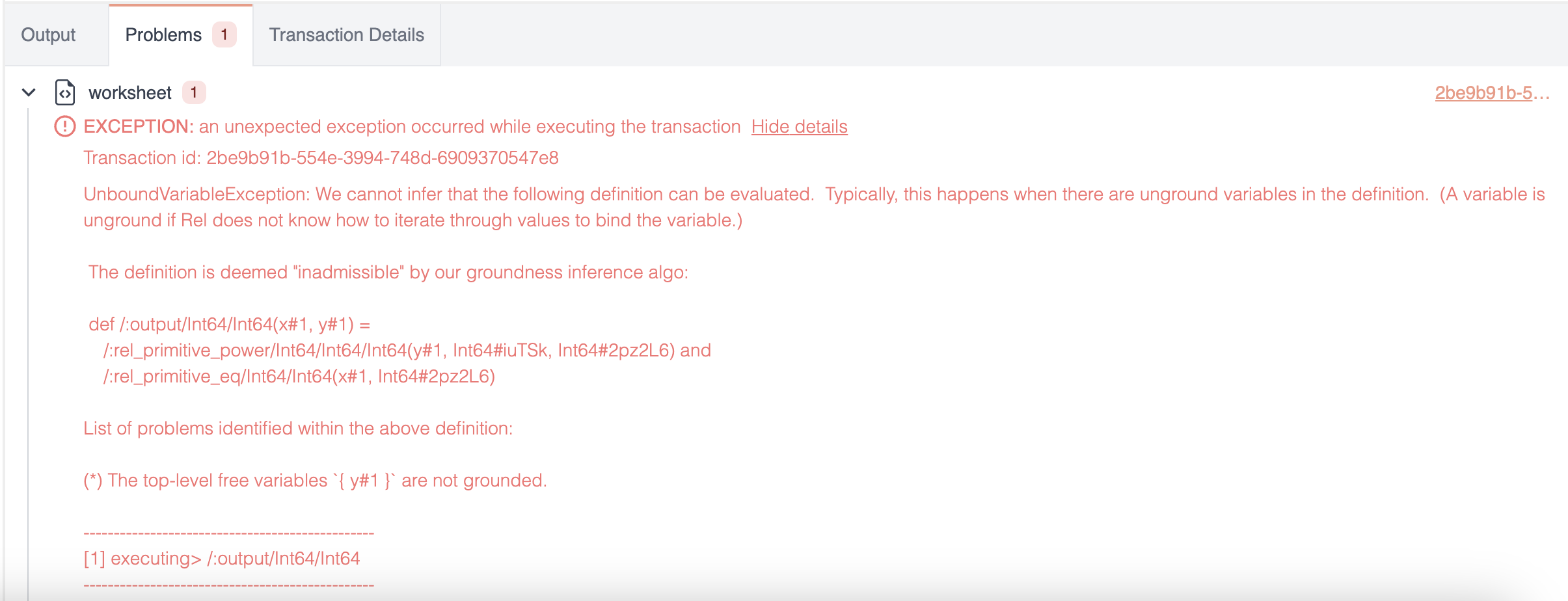
The code above leads to an ungrounded variable error because the equation y^2=x is nonlinear. In this case, the valid values for y are known to be 2 and -2, yet the system can’t resolve this due to the nonlinear nature of the equation.

One solution is to rewrite the equation such that it’s linear in y (if possible):

// read query
 
def output(x, y) {
    x = 4
    and (y = sqrt[x] or y = -sqrt[x])
}

Or you can provide an explicit finite domain for y:

// read query
 
def D = range[-10, 10, 1]
 
def output(x, y in D) {
    x = 4
    and y^2 = x
}

In this way, the mathematical equation turns into a filter and only keeps (x, y) pairs that fulfill the equation.

See Grounded Variables in the Rel Language Reference manual and Rel Primer: Advanced Syntax for more details.