Integrity Constraints

Integrity constraints ensure the accuracy and consistency of data in a relational database. In this guide, you’ll learn why you should use integrity constraints, when it makes sense to use them, and how to write them in Rel.

Introduction

Integrity constraints (ICs) verify that data in a relational database conform to a standard of correctness. You can use ICs to guarantee that performing data insertions, updates, and other processes don’t affect the integrity of the data.

The syntax for ICs is similar to the syntax for any relation in Rel:

// read query
 
ic check_string(s in R) {
    String(s)
}

Instead of def, IC definitions start with the keyword ic. Parameters may be inserted between parentheses after the name of the IC, and those parameters can be bound using the same techniques available for binding parameters in definitions of relations, including relational abstraction and relational application. The complete syntax for integrity constraints can be found in Integrity Constraints in Rel Reference.

There are three general categories of integrity constraints:

1. Type constraints ensure that data have the correct data type, such as String or Int. These constraints are inherent to the data model and can usually be evaluated statically.
2. Value constraints ensure that individual entries in a relation hold a specific value or lie within a specific range.
3. Logical constraints ensure that relations adhere to specific logical rules and can express expert knowledge in RelationalAI’s Relational Knowledge Graph System (RKGS).

Basics

You define an IC with the ic keyword, followed by a name and an expression enclosed in curly brackets. The IC expression must evaluate to either true or false.

The following example defines a nums relation and an integrity constraint that ensures nums contains only positive numbers:

// model
 
def nums = {1; 2; 3}
 
ic positive_nums {
    forall(x:
        nums(x)
        implies
        x > 0
    )
}

ic {
  forall(x:
      nums(x)
      implies
      x > 0
  )
}

When you define an IC, the system creates an IC relation. This IC relation is the negation of the expression in the body of the IC.

The IC relation for the positive_nums IC is:

not forall(x: nums(x) implies x > 0)

Logically, this is equivalent to:

exists(x: nums(x) and not x > 0)

An IC is violated when its IC relation is nonempty. For example, inserting a negative integer into nums violates the positive_nums IC:

// read query
 
def nums = -1
def output = nums

In the RAI Console, you see a red error message with the ICs violation report:

However, the output of this query may look surprising:

ICs prevent tuples that violate the IC from getting inserted into a relation. So why does -1 appear in nums?

To understand why, it helps to understand how the transaction works. Executing the preceding query creates a transaction where nums becomes the relation {-1; 1; 2; 3}. Then the positive_nums IC runs against this transaction.

The expression in the IC body is false since num contains a negative number. Thus the IC relation, which is the negation of the IC expression, evaluates to true. In Rel, true is represented by the relation {()}. Since {()} is nonempty, this violates the positive_nums IC and the transaction aborts.

The output displays the contents of nums from the aborted transaction, not the state of nums after the transaction aborts. You can confirm that nums hasn’t been altered in a new query:

// read query
 
def output = nums

Indeed, nums contains only the numbers 1, 2, and 3, as expected.

Inspecting the output of an aborted transaction may be useful for determining why an IC was violated, but there is a better way: Write ICs with parameters.

For instance, here’s one way to write positive_nums with a parameter in its header:

// read query
 
ic positive_nums(x) {
    nums(x)
    implies
    x > 0
}

When you add parameters to an IC, its IC relation gets the same parameters. Thus, if positive_nums is violated, its IC relation contains the values for x that violate the constraint.

Binding IC Parameters

When you write ICs with parameters, those parameters must be bound (opens in a new tab) to a finite domain. Parameters that aren’t bound result in an UNBOUND_VARIABLE error.

For example, you may be tempted to write the positive_nums IC as:

// read query
 
ic positive_nums(x) {
    nums(x)
    and
    x > 0
}

Executing this query in the Editor results in two errors:

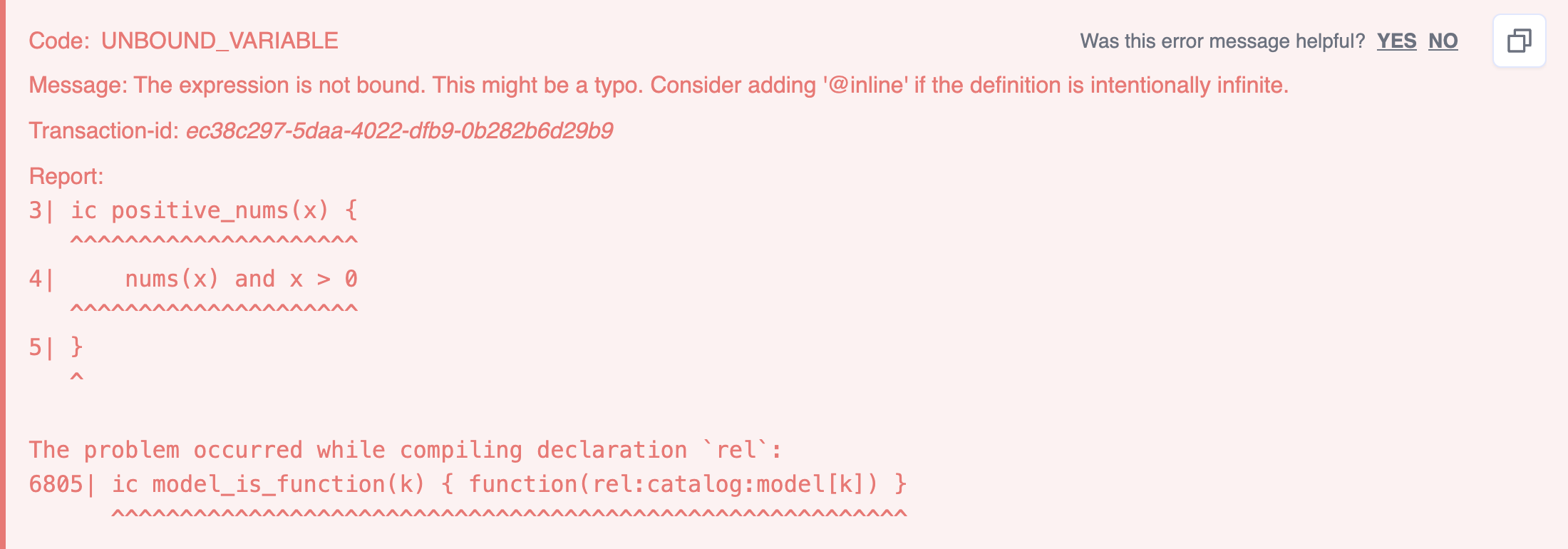
The errors tell you that:

• The IC is violated.
• The variable x is unbound.

At first glance, this might be surprising, because all values of x in nums fulfill the condition x > 0. However, because an IC relation is the negation of the IC expression, the IC relation for positive_nums is equivalent to the following relation:

{x: not (nums(x) and x > 0)}

There are infinitely many values of the variable x that make the statement not (nums(x) and x > 0) true. In particular, nothing here says that the values of x must be in nums. Values like x = -1 or x = "abc" are valid counterexamples that violate the IC.

Typically, IC parameters are bound using either the implies or the in keywords.

Using the implies Keyword

You can bind parameters using relational application and implies (opens in a new tab). This is how the parameter is bound in the positive_nums IC from the previous section:

// read query
 
ic positive_nums(x) {
    nums(x)
    implies
    x > 0
}

The relational application nums(x), when used on the left-hand side of a logical implication, binds x to the domain nums.

Using the in Keyword

Another way to bind IC parameters is with the in keyword. Using in, you can rewrite the positive_nums IC as follows:

// read query
 
ic positive_nums(x in nums) {
    x > 0
}

Here, x is bound to the domain nums with in. Note that the binding is done in the IC header. In many cases, this style of binding is preferable since it leads to shorter IC bodies.

Integrity Constraints in Modules

Integrity constraints can be placed within modules. For example:

// read query
 
module Tool
    def ItemID = {1; 2; 3}
    def name = {(1, "Power Drill"); (2, "Jigsaw"); (3, "Hammer")}
    def price = {(1, 100.0); (2, 50.0); (3, 20.0)}
 
    ic require_name_price(i in ItemID) {
        name(i, _) and price(i, _)
    }
end

This example triggers an IC violation if any item is missing a name or a price.

You more details, see Integrity Constraints in Modules in the Modules concept guide.

Common Use Cases

There are three main reasons to use ICs:

1. To ensure integrity of the data in a database across multiple transactions .
2. To check the integrity of data in a single transaction.
3. To check the correctness of intermediate results in a complex query.

The difference between ensuring integrity and checking integrity has to do with the lifetime of the integrity constraint:

• ICs that are installed as Rel models ensure the integrity of data because all future transactions are checked against the IC.
• ICs in write and read queries do not persist beyond the lifetime of the transaction that contains them. These ICs check the integrity of the data for that single transaction.

For example, you may install an IC that ensures that tuples in a base relation have the correct data types. In these cases, you may install the ICs before any data have been inserted into the database.

On the other hand, a query that computes new values from data in various relations may include an IC to check that the computation was performed correctly.

Further Examples

SQL users may be familiar with integrity constraints that ensure columns in a SQL table contain unique values, or that columns don’t contain any null values. ICs in Rel can express similar constraints on data. However, the ability to model complex relations in Rel makes ICs more powerful than their SQL counterparts.

This section explores three categories of ICs: type constraints, value constraints, and logical constraints.

Logical constraints go beyond traditional SQL integrity constraints by enforcing domain knowledge that can’t be expressed by type and value constraints alone.

Type Constraints

Type constraints ensure that data have the correct data type, such as String or Int.

For example, consider the following person relation with a :name property:

// write query
 
def name:first = {
    (1, "Fred");
    (2, "David");
    (3, "Brian");
    (4, "Jacques");
    (5, "Julie");
}
 
def name:last = {
    (1, "Smith");
    (2, "Johnson");
    (3, "Williams");
    (4, "Brown");
    (5, "Jones");
}
 
def insert:person:name = name

Each tuple in person:name:first and person:name:last contains an ID and a name. The ID should be an Int and the name should be a String. The following ICs enforce these types:

// read query
 
ic first_name_types(id, x) {
    person:name:first(id, x)
    implies
    Int(id) and String(x)
}
 
ic last_name_types(id, x) {
    person:name:last(id, x)
    implies
    Int(id) and String(x)
}

Note that the IC parameters are such that any tuples in person:name:first and person:name:last that don’t conform to the type constraints are returned as counterexamples.

Alternatively, you may write an IC to enforce these types on both of the :first and :last subproperties simultaneously:

// read query
 
ic person_name_types(subproperty, id, x) {
    person:name[subproperty](id, x)
    implies
    Int(id) and String(x)
}

In fact, person_name_types ensures that any subproperty of person:name conforms to the type constraints. Suppose you add another subproperty called person:name:MI to store the person’s middle initial. Then values in :MI must have type String to avoid violating the IC. For instance, you couldn’t store them as Char without violating or modifying the IC.

The @static Annotation

Type ICs can often be evaluated statically, based only on the schema, without having to actually evaluate the relation. You can use the @static annotation to tell the RKGS that you expect that an IC can be statically evaluated:

// read query
 
@static
ic person_name_types(subproperty, id, x) {
    person:name[subproperty](id, x)
    implies
    Int(id) and String(x)
}

Annotating type ICs with @static may improve performance, especially if the model has many type constraints.

Value Constraints

Value constraints ensure that the values of individual entries in a relation adhere to certain conditions.

For example, consider the person:name relation from the previous section:

def person:name:first = {
    (1, "Fred");
    (2, "David");
    (3, "Brian");
    (4, "Jacques");
    (5, "Julie");
}
 
def person:name:last = {
    (1, "Smith");
    (2, "Johnson");
    (3, "Williams");
    (4, "Brown");
    (5, "Jones");
}

Each person’s ID should be positive:

// read query
 
ic id_is_positive(subproperty, id) {
    person:name[subproperty](id, _)
    implies
    id > 0
}

// read query
 
ic id_is_positive(subproperty, id) {
    person:name[subproperty](id, Any)
    implies
    id > 0
}

This IC checks that the IDs in every subproperty of person:name are positive. Counterexamples that violate the IC contain the name of the subproperty and the ID of the person. The id_is_positive IC has a weakness, however: It only checks tuples with arity 2.

One way to ensure that all tuples, regardless of their arity, contain a positive integer in the first position is to use the Standard Library’s first relation:

// read query
 
ic id_is_positive(subproperty, id) {
    first[person:name[subproperty]](id)
    implies
    id > 0
}

You may also write value constraints that enforce a particular arity. For example, the following IC ensures that every subproperty of person:name has arity 2:

// model
 
ic person_name_arity(subproperty in first[person:name], x) {
    arity[person:name[subproperty]] = x
    implies
    x = 2
}

// read query
 
def R = {
    1;
    (2, 3);
    (4, 5, 6);
}
 
def output = arity[R]

Logical Constraints

Logical constraints ensure that relations adhere to specific logical rules. They serve not only as a way to check the correctness of data, but also express expert knowledge.

Logical constraints, among other things, may check that:

• Certain entries in a relation contain unique values.
• One relation is a subset of another.
• Two or more relations are disjoint.
• A relation is symmetric or transitive.

In the following sections, you’ll continue to add new properties to the person relation and write logical constraints that express rules about those properties and relationships between them.

Unique Value

In Rel, you can write integrity constraints that ensure the values in a particular component of tuples in a relation are unique. These unique value constraints are similar to PRIMARY KEY and UNIQUE constraints on a column in a SQL database.

PRIMARY KEY-Like Constraints

In SQL, PRIMARY KEY constraints ensure that no two rows in a SQL table have the same primary key, typically an integer ID. These kinds of constraints are also possible in Rel.

Consider again the person:name:first relation from the previous sections:

def person:name:first = {
    (1, "Fred");
    (2, "David");
    (3, "Brian");
    (4, "Jacques");
    (5, "Julie");
}

Each person should have exactly one first name. In other words, each tuple should begin with a unique ID. The following IC uses count to ensure that the number of tuples that begin with a particular ID is 1:

// read query
 
ic unique_id(id, x) {
  count[person:name:first[id]] = x implies x = 1
}

Counterexamples that violate the IC contain an id and the number x of tuples that begin with id.

ic unique_id(id) {
    count[person:name:first[id]] = 1
}

Since the person:name:first relation has arity 2, you may also check the uniqueness of each person’s ID using the built-in function relation:

// read query
 
ic unique_id {
    function[person:name:first]
}

The preceding IC works by ensuring that every ID maps to a unique name. Inserting the tuple (5, "Hari"), for example, violates the IC since person:name:first already contains (5, "Julie"). However, the RKGS won’t report counterexamples because the IC has no parameters.

One way to write the IC with parameters is to check that if name1 and name2 are any two first names associated with the same ID, then name1 = name2 must hold:

// model
 
ic unique_id(id) {
    forall(name1, name2:
        person:name:first(id, name1) and person:name:first(id, name2)
        implies
        name1 = name2
    )
}

Counterexamples that violate the IC contain the id values that map to two or more names. For example, if the tuples (6, "Hari") and (6, "Salvor") are both contained in person:name:first, then 6 is a counterexample.

Note, however, that this IC doesn’t prevent tuples with different arities from beginning with the same ID. The tuples (5, "Julie") and (5, "Julie", "Mao") can both be present in the relation, for instance. That’s because the IC only checks tuples of arity 2 and ignores everything else.

UNIQUE-Like Constraints

Consider the following relation that assigns an email address to an ID:

// write query
 
def email = {
    (1, "fred@example.com");
    (2, "david@example.com");
    (3, "brian@example.com");
    (4, "jacques@example.com");
    (5, "julie@example.com");
}
 
def insert:person:email = email

No two people should have the same email address. In a SQL database, you express this by adding a UNIQUE constraint to the column that stores email addresses. In Rel, you must write an IC that ensures that a particular element of each tuple — in this case, the second element — contains unique values.

One way to do this is to check that the frequency of each email address is 1:

// read query
 
ic unique_email(email, freq) {
    frequency(person:email, email, freq)
    implies
    freq = 1
}

Any email address that appears multiple times in the relation violates the unique_email IC. Counterexamples contain both the email address and its frequency.

Alternatively, counterexamples to the following IC contain the ID and email address of duplicates:

// read query
 
ic unique_email(id, email) {
    person:email(id, email)
    implies
    frequency(person:email, email, 1)
}

Note that both of the preceding ICs rely on the fact that the arity of person:email is 2. Writing ICs that ensure unique values in an arbitrary component of each tuple, regardless of the arity, may be messy. One of the benefits of keeping relations in Graph Normal Form is that ICs are easier to write.

Subset

A relation is a subset of another relation if each tuple in the first relation is also a tuple in the second. You can check if one relation is a subset of another using the Standard Library’s built-in subset relation.

To illustrate this, you can define a :gender property on person that assigns each person’s ID to a Char representing their gender — 'M' for male, 'F' for female, and 'X' for nonbinary:

// write query
 
def gender = {
    (1, 'M');
    (2, 'M');
    (3, 'F');
    (4, 'F');
    (5, 'X');
}
 
def insert:person:gender = gender

Every person must be assigned one of the characters 'M', 'F', or 'X'. To that end, you can define a valid_genders relation containing those characters:

// model
 
def valid_genders = {'M'; 'F'; 'X'}

The following IC ensures that the set of second elements of each tuple in person:gender is a subset of the valid_genders relation:

// read query
 
ic gender_is_valid {
    subset(second[person:gender], valid_genders)
}

ic gender_is_valid {
  second[person:gender] ⊆ valid_genders
}

The RKGS won’t report counterexamples for the gender_is_valid IC, since it has no parameters. Here’s one way to write the IC with parameters:

// model
 
ic gender_is_valid(id) {
    forall(x:
        person:gender(id, x)
        implies
        valid_genders(x)
    )
}

This IC ensures that if (id, x) is a tuple in person:gender, then x is also a valid gender. Counterexamples contain the id of the person with an invalid gender character.

Note that neither of the implementations of gender_is_valid check that each person is actually assigned a gender. For instance, inserting a singleton such as (6,) into person:gender doesn’t violate the IC.

Disjoint Relations

Two relations are disjoint if they have no tuples in common. You can check whether or not two relations are disjoint using the built-in disjoint relation.

ICs that test for disjointness can be used to express expert knowledge about relationships between entities in the database. For example, suppose you have a set of organizations stored in your database:

// write query
 
def organization_name = {
    (1, "Organization A");
    (2, "Organization B");
    (3, "Organization C");
}
 
def insert:organization:name = organization_name

The following relations assign people from the person relation to organizations of which they are members:

// write query
 
def member_of_organization = {
    (1, 1);
    (1, 2);
    (2, 2);
    (2, 3);
    (3, 3);
    (4, 3);
    (5, 1);
}
 
def insert:member_of = member_of_organization

// model
 
def member_of_A(id) = member_of(id, 1)
def member_of_B(id) = member_of(id, 2)
def member_of_C(id) = member_of(id, 3)

The three derived relations member_of_A, member_of_B, and member_of_C contain the IDs of people who are members of each of the three organizations. Defining these derived relations makes reasoning about organizational membership easier when writing queries and ICs.

One person may be a member of multiple organizations. But, suppose that members of Organization A aren’t allowed to be members of Organization C. The following IC checks that the set of people who are members of Organization A is disjoint from the set of people who are members of Organization C:

// read query
 
ic membership_check {
    disjoint(member_of_A, member_of_C)
}

The RKGS won’t report any counterexamples that violate the preceding IC, since it has no parameters. To address this, the following IC explicitly checks that a member of Organization A isn’t a member of Organization C:

// read query
 
ic membership_check(id) {
    member_of_A(id)
    implies
    not member_of_C(id)
}

For example, inserting the tuple (1, 3) into the member_of relation violates the IC because member_of also contains the tuple (1, 1). The system computes derived relations on the fly, so inserting (1, 3) into member_of means that both member_of_A and member_of_C contain the ID 1.

Symmetry

The following relation pairs people from the person relation with their friends:

// write query
 
def friends = {
    (1, 2);
    (1, 5);
    (2, 1);
    (3, 4);
    (4, 3);
    (5, 1);
}
 
def insert:is_friends_with = friends

A tuple (x, y) contained in is_friends_with indicates that person x is friends with person y. Naturally, such a relationship should be symmetric. If x is friends with y, then y is also friends with x.

The following IC ensures that is_friends_with is symmetric by checking that the transpose relation — the relation derived from is_friends_with by reversing all of the pairs — is equal to the original relation:

// read query
 
ic is_symmetric {
    equal(is_friends_with, transpose[is_friends_with])
}

You can also ensure that a relation is symmetric using an IC with parameters:

// read query
 
ic is_symmetric(id1, id2) {
    is_friends_with(id1, id2)
    implies
    is_friends_with(id2, id1)
}

Transitivity

You can begin by defining a property person:dob that contains the year of birth for each person, and an is_older relation containing pairs (a, b) where person a is older than person b:

// write query
 
def date_of_birth = {
    (1, 1984);
    (2, 1990);
    (3, 1974);
    (4, 1994);
    (5, 1999);
}
 
def insert:person:dob = date_of_birth

// model
 
def is_older(id1, id2) = {
    person:dob[id1] < person:dob[id2]
}

If person a is older than person b, and person b is older than person c, then it must be the case that person a is also older than person c. This is an example of a transitive relation.

The following IC checks that is_older is transitive:

// read query
 
ic is_transitive(id1, id2, id3) {
    is_older(id1, id2) and is_older(id2, id3)
    implies
    is_older(id1, id3)
}

There is a more compact way to check transitivity using the dot join operator:

// read query
 
ic is_transitive {
   is_older.is_older ⊆ is_older
}

This IC checks that the composition is_older.is_older is a subset of is_older. You can think of composition as joining tuples together on common last and first elements. In other words, if (x, y) and (y, z) are tuples in is_older, then is_older.is_older contains the tuple (x, z). See the Advanced Syntax section of the Rel Primer to learn more about composition.

The preceding version of is_transitive has no parameters, but you can fix this by using implies instead of the ⊆ operator:

// read query
 
ic is_transitive(id1, id2) {
   is_older.is_older(id1, id2)
   implies
   is_older(id1, id2)
}

A relation that doesn’t have to be transitive is the is_friends_with relation from the Symmetry section. Just because a is friends with b and b is friends with c doesn’t mean that a is friends with c.

In fact, is_friends_with isn’t transitive, and you can verify this with the following IC:

// read query
 
ic is_transitive_friends(id1, id2, id3) {
    is_friends_with(id1, id2) and is_friends_with(id2, id3)
    implies
    is_friends_with(id1, id3)
}

Person 5 is friends with person 1 and person 1 is friends with person 2, but person 5 isn’t friends with person 2, and this violates the is_transitive_friends IC.

Integrity Constraint Violations

The RKGS aborts any transaction that violates an IC and reports the violation in two ways:

1. Console violation reports display information about IC violations in the RAI Console.
2. The built-in abort relation for a transaction is set to true.

This section describes both IC violation reporting mechanisms in detail.

Console Violation Reports

In the Basics section, you saw the following example of an IC violation report:

The RAI Console displays IC violation reports after a transaction that violates an IC aborts. These reports are presented as red error boxes and include the following information:

• The name and definition of the violated IC.
• The transaction ID of the transaction that violated the IC.

The abort Relation

When an IC is violated, the abort relation is automatically set to true for the transaction that caused the violation.

Consider the nums relation and the positive_nums IC from the previous section:

// model
 
def nums = {1; 2; 3}
 
ic positive_nums(x) {
    nums(x)
    implies
    x > 0
}

Extending nums with a negative integer violates the positive_nums IC and, as a result, the transaction aborts:

// read query
 
def nums = -1
def output:aborted = abort

Case Study: Mini-IMDb Dataset

This section uses the Mini-IMDb data as an example of a real-world dataset and shows how ICs can enforce a schema and encode expert knowledge in your database.

Load the Data

The Mini-IMDb dataset consists of three CSV files:

1. name.csv contains the names of actors.
2. title.csv contains the titles of movies.
3. cast_info.csv pairs actors with movies they have appeared in.

The following Rel code defines schemas for each of the three CSV files and uses the load_csv relation to import the data into the RKGS:

// write query
 
def url = "azure://raidocs.blob.core.windows.net/datasets/imdb/"
 
module config_name
    def path = concat[url, "name.csv"]
    def schema = {
        (:person_id, "int");
        (:name, "string");
    }
end
def insert:name_csv = load_csv[config_name]
 
module config_title
    def path = concat[url, "title.csv"]
    def schema = {
        (:movie_id, "int");
        (:title, "string");
        (:year, "int");
    }
end
def insert:title_csv = load_csv[config_title]
 
module config_cast_info
    def path = concat[url, "cast_info.csv"]
    def schema = {
        (:movie_id, "int");
        (:person_id, "int");
    }
end
def insert:cast_info_csv = load_csv[config_cast_info]

For more information about loading CSV files, including working with schemas, see the CSV Import how-to guide.

Next, define relations to access the data in Rel:

// model
 
def movie:title = title_csv:movie_id[pos], title_csv:title[pos] from pos
def movie:year = title_csv:movie_id[pos], title_csv:year[pos] from pos
def movie:id = first[movie[_]]
 
def actor:name =  name_csv:person_id[pos], name_csv:name[pos] from pos
 
def cast = cast_info_csv:movie_id[pos], cast_info_csv:person_id[pos] from pos
 
def co_actors(id1, id2) =
    cast(movie_id, id1)
    and cast(movie_id, id2)
    and id1 != id2
    from movie_id

Now you’re ready to write some ICs.

Define Integrity Constraints

In previous examples in this guide, you defined ICs in query transactions. However, ICs in queries don’t persist beyond the transaction’s lifetime. In this example, you’ll install ICs so that they run against all future queries.

First, you can check that the actor name is a String and the actor identifier is an Int:

// model
 
@static
ic actor_type_check(id, name) {
    actor:name(id, name)
    implies
    Int(id) and String(name)
}

For brevity, this example contains only one type constraint. In general, however, you should write ICs that check all of the data types in the database. This ensures that future transactions that update the data, or insert new data, don’t introduce inconsistent types.

You can use ICs to insert expert knowledge into a database. For instance, the oldest entry in IMDb is the documentary “Passage de Venus” made in 1874. You can add an IC to check that no movie year is earlier than 1874:

// model
 
ic min_movie_year(id, year) {
    movie:year(id, year)
    implies
    year >= 1874
}

The co_actors relation should be symmetric. The following IC checks that this is true:

// model
 
ic co_actors_symmetric(actor1, actor2) {
    co_actors(actor1, actor2)
    implies
    co_actors(actor2, actor1)
}

The RKGS doesn’t report an IC violation when you execute the preceding query so, indeed, co_actors is symmetric.

The Mini-IMDb dataset is small, so there are relatively few ICs that you need to write. As a dataset grows, the need for integrity constraints also grows, to ensure that the knowledge graph stores data in a correct and consistent manner.

Best Practices

This section describes some best practices for writing ICs so that you have the most actionable information at hand when an IC is violated.

Use Named Integrity Constraints

You can give ICs descriptive names, even though anonymous ICs are perfectly valid. The RKGS assigns unique identifiers to ICs without user-defined names, which can make it difficult to know which IC a transaction violates.

Consider the following toy example:

// read query
 
ic (id) {
    id = {1;2;3}
    implies
    id <= 2
}
 
ic (id) {
    id = {1;2;3}
    implies
    id < 2
}

Both ICs are violated. However, the only way to distinguish which IC is which is with the system-generated identifier. In such situations, it may be impossible to know exactly which IC was violated.

Define Integrity Constraints With Parameters

You can use parameters in IC definitions so that the RKGS reports counterexamples whenever a transaction violates the IC. For example, consider the following example with two equivalent ICs — one with parameters and one without:

// read query
 
def person:age = {
    (1, 37);
    (2, 31);
    (3, 47);
    (4, 27);
    (5, 12);
}
 
ic with_parameters(id, age) {
    person[:age](id, age)
    implies
    age >= 18
}
 
ic without_parameters {
    forall(id, age:
        person[:age](id, age)
        implies
        age >= 18
    )
}

Both ICs are violated because person 5 has age 12, and 12 is less than 18.

Tips and Tricks

Interpreting IC Warnings

You may encounter a NON_EMPTY_INTEGRITY_CONSTRAINT warning. This warning alerts you about cases where an IC is trivially satisfied whenever a relation is empty, but it’s not an error and, in some cases, you can ignore the warning.

Consider the following IC:

// read query
 
def R = {1; 2; 3}
 
ic check_float {
    forall(id:
        R(id)
        implies
        Float(id)
    )
}

This query produces an INTEGRITY_CONSTRAINT_VIOLATION error, as well as a NON_EMPTY_INTEGRITY_CONSTRAINT warning:

If R were empty, then the IC would be trivially satisfied. That is, if there are no items in R, then they’re all of type Float — or any other type, for that matter. This may not be what you intended to write, which is why you see a warning.

This warning can also appear when you expect a relation to be empty, such as the :load_errors relation after importing a CSV file. In these cases, you can safely ignore the warning.

Deactivating Integrity Constraints

You can deactivate integrity constraints by adding :disable_integrity_constraints to the relation rel:config:

// write query
 
def insert:rel:config = :disable_integrity_constraints

Once the transaction completes, the RKGS ignores all ICs, including all previously installed ICs and any future ones. Although you should use this feature with care, it can be useful, for example, to improve performance if very expensive ICs are present.

You can also deactivate ICs for an individual query executing it as a read query. Therefore, the insert declaration to deactivate the ICs only applies to the current transaction lifetime, i.e., it is not persisted in the database:

// read query
 
def insert:rel:config = :disable_integrity_constraints
 
def R = {1; 2; 3}
ic { count[R] = 7 }

Any installed ICs remain active for future transactions after the preceding transaction terminates.

You can reenable ICs by deleting that configuration for :disable_integrity_constraints:

// write query
 
def delete:rel:config = :disable_integrity_constraints

Summary

Integrity constraints are a set of rules that ensure the accuracy of data in your database. They are categorized into type, value, and logical constraints. You can install integrity constraints as Rel models so that they check every transaction, or you can use them in a read query to check query results or intermediate steps.

Understanding how ICs work allows you to interpret IC violation reports and helps you maximize their effectiveness to avoid common pitfalls.