Bound Declarations

Overview

A bound declaration allows you to specify the schema of a relation, as well as to impose various constraints on selected relations.

This is especially useful if the specified relation is a relation that is not yet defined. It is common for a base relation to be created only at runtime, when its contents are loaded into the system. The application logic that uses and transforms the data in the base relation is often written beforehand. Since the logic refers to the base relation, the compiler cannot fully perform certain operations — such as checking type correctness or optimizations — until the base relation is created. This means that various errors cannot be detected until runtime. Even if there are no errors, you may want to forego the performance cost of this runtime compilation.

Skillful use of bound declarations can help get more work done at compile time. Moreover, a bound declaration provides a place for adding annotations and docstrings to a base relation that has not yet been created.

Bound declarations are not intended only for base relations. They are useful in other contexts, too. In general, they can provide redundancy that allows the compiler to detect errors in complex logic. For instance, if the bound declaration constrains the type of a relation to something that is incompatible with the type inferred by the compiler, then you must inspect your logic to restore consistency. It is much cheaper and more effective to find and fix such errors during development than in the course of field operations.

The contents of base or derived relations can change during runtime. So, to ensure compliance between relations and bound declarations at all times, the compiler generates appropriate integrity constraints. In this way, you can view bound declarations as a convenient way to introduce certain kinds of integrity constraints that can also be exploited by the system.

Syntax and Semantics

Declaration :=
    Annotation* "bound" BoundDeclLeftHandSide (BoundDeclRightHandSide)?
 
BoundDeclLeftHandSide = Id FormalParamsBracket* FormalParamsParen?
 
BoundDeclRightHandSide = "=" Expr | "{" Expr "}"

A bound declaration looks very much like a definition, except that:

• The keyword bound is used instead of def.
• The right-hand side is optional.
• The expression on the right-hand side must not be higher-order or recursive.

Note that in this section the term “relation” is used in the narrow sense of “standard relation”, that is, it refers to a set of tuples that have the same type. In Rel a number of different relations can share the same name.

Roughly speaking, the semantics of bound declarations are as follows:

1. Let B be a bound declaration:

   • B applies only to relations named by the left-hand side.

     bound R = Int, String

     This bound declaration applies only to relations named R.

   • The left-hand side may also specify details about the arity and the type of the relations to which the bound declaration applies. A relation that meets the specified criteria is said to match the bound declaration B.

     bound R(x, y)

     Here, the bound declaration is matched only by relations whose name is R and whose arity is 2.

   • The right-hand side of B specifies some relation RB.

     bound R = Int, String
     bound T(x, y) {Int(x) and Float(y) and y > 0.5}

     Here, R is required to be a relation with the signature (Int, String). A binary relation T is required to have the type signature (Int, Float) and the floating-point numbers in the first column are required to be larger than 0.5.

     If B does not have a right-hand side, then RB is {x... : true}, that is, the union of all possible relations.

     bound R

     The relation R has no conditions attached.

   • B places a bound on the relations that match it. More specifically, a relation that matches B is said to be allowed by B if it is a subset of RB.

     bound R(x in Int, y in String) {x > 0 and contains(y, "abc")}

     If a relation R has the signature (Int, String), then all its tuples are required to have positive integers, and their second elements should contain the sequence “abc”.

2. If there are no bound declarations that apply to a relation, the relation is allowed.

   bound R(x in Int, y in Int) { y > x }
    
   def R = (1, -1.0)

   The relation R shown here is allowed, because the second column is of type Float and not Int.

3. If a relation matches at least one bound declaration, then it is allowed if it is allowed by the union of the bound declarations that it matches.

   Consider the following example:

   bound R(x, y) { x > y }
   bound R(x, y) { x < 9 }
   bound R = String, Int
    
   def R = { (1, 1); (20, 10) }
   def R = { ("1a", 2) }

   Each of the two relations named R — one whose type is (Int, Int) and one whose type is (String, Int) — is allowed.

   The relation whose type is (String, Int) matches all three bound declarations. It is allowed only by the third.

   The relation whose type is (Int, Int) matches the first two bound declaration. The tuple (1, 1) is allowed only by the second bound declaration and the tuple (20, 10) is allowed only by the first bound declaration. The entire relation is allowed by the union of these bound declarations: bound R(x, y) { x > y ; x < 9 }.

If a relation R is not allowed, then it will cause a violation of one or more integrity constraints generated from the bound declarations. Some of the tuples in R may be consistent with these integrity constraints. In that case you can say that each such tuple is allowed.

If you remove one of the bound declarations in the example above, you violate the integrity constraints generated from the other two. In particular, if you remove the first bound declaration, then the tuple (20, 10) is allowed, but the tuple (1, 1) causes an IC violation.

Examples

Imagine that you are writing logic that refers to a base relation B. The base relation will be loaded at runtime, but you want to test your logic first. For example, you may want the relation P to contain information about whether B is already defined:

def P("yes") = B[_]
def P("no")  = not B[_]
 
def output = P

This works well, but you also get a warning that looks like this:

In order to suppress the warning, you can simply declare that there will be a relation called B:

// read query
 
bound B
 
def P("yes") = B[_]
def P("no")  = not B[_]
 
def output = P

This simple bound declaration does not say anything about the type of B. If you know that B will be a binary relation, each of whose tuples contains an integer followed by a string, you can declare this as follows:

bound B = Int, String

The declaration literally means that the relation B is bound to be a subset of Int, String. The expression Int, String denotes the Cartesian product of the relations Int and String.

You can test the effect of such a declaration on another relation, R, as follows:

// read query
 
bound R = Int, String
 
def R = (65, "A"); (97, "a"); ("b", 66)
 
def output = R

The entire contents of relation R — or, rather, of the two relations that share the name R — are shown, but you will also see the following:

The compiler generated the integrity constraint from the bound declaration.

The right-hand side of a bound declaration can express the requirement that a relation be a subset of arbitrary relations, not necessarily type relations such as Int or String. Here is a simple example:

bound R = range[0, 9, 1]
 
def R = range[1, 11, 1]

Another example:

def PA = { 1; 2; 3 }
def PB = { ("a", "A"); ("b", "B"); ("c", "C") }
def PC = { "lower"; "upper" }
 
bound R = PA, PB, PC
 
def R = { (2, "b", "B", "upper"); (3, "d", "D", "lower")}

Since ("d", "D") is not in PB, you will see:

If you want your relation to contain only positive integers, you can express it with a bound declaration:

bound R(x) { Int(x) and x >= 0 }

The right-hand side specifies the relation that contains all the positive integers. In other words, the bound declaration expresses the constraint “only positive integers are allowed.” Note, however, that the constraint applies only to a unary relation R. You can think of it as applying only to relations that match the left-hand side of the bound declaration. A relation R whose arity is different from 1 is allowed, and can contain both negative integers and data items of other types:

bound R(x) { Int(x) and x >= 0 }
 
def R = 2; 0; -1; "a"         // Unary
def R = (-3, "X"); (3, "Y")   // Binary
def R = ("Y", -1, 5.0)        // Ternary

There are two unary relations, both named R: one that contains integers, and one that contains strings. So the warning looks like this:

Another way to express the requirement about positive integers is this:

bound R(x in Int) { x >= 0 }

The effect is subtly different. The constraint applies not to all unary relations whose name is R, but only to those that contain integer elements. The left-hand side of the declaration does not match unary relations that contain elements of other types. So there is no IC violation for "a":

bound R(x in Int) { x >= 0 }
 
def R = 2; 0; -1; "a"         // Unary
def R = (-3, "X"); (3, "Y")   // Binary
def R = ("Y", -1, 5.0)        // Ternary

If you extend this example by adding bound R(x in Int), you will thereby declare that there is also a unary relation R that has integer elements but no constraints. The two bound declarations will be equivalent to their union, bound R(x in Int) = x >= 0 or true, so the example will not result in an IC violation.

A third example on the same theme:

bound R[x in Int] { x >= 0 }
 
def R = 2; 0; -1; "a"         // Unary
def R = (-3, "X"); (3, "Y")   // Binary
def R = ("Y", -1, 5.0)        // Ternary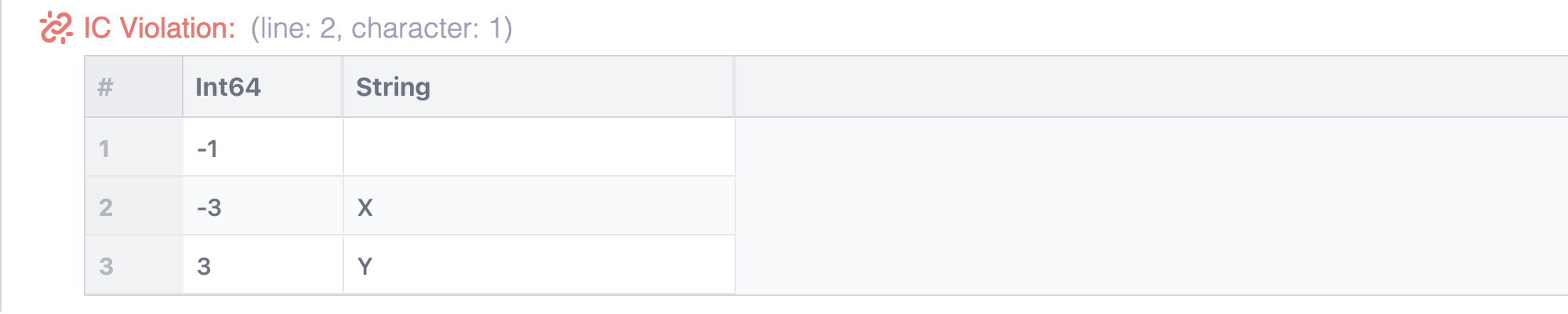

The difference is in the square brackets. The left-hand side matches every relation whose name is R, whose arity is at least 1, and whose first column is integer. The right-hand side, in this case, not only requires x to be positive, but also does not leave room for more elements, since the result of projecting away the first column is a nullary relation: either true or false. In other words, the bound declaration means that the relation that matches the left-hand side must be unary. So tuples (-3, "X") and (3, "Y") are not allowed; ("Y", -1, 5.0), however, is allowed, because the first element is not an integer.

In order to allow binary relations, you could write bound R[x in Int] = x >= 0, Any. But this would require all matching relations to be binary:

bound R[x in Int] { x >= 0, Any }
 
def R = 2; 0; -1; "a"         // Unary
def R = (-3, "X"); (3, "Y")   // Binary
def R = ("Y", -1, 5.0)        // Ternary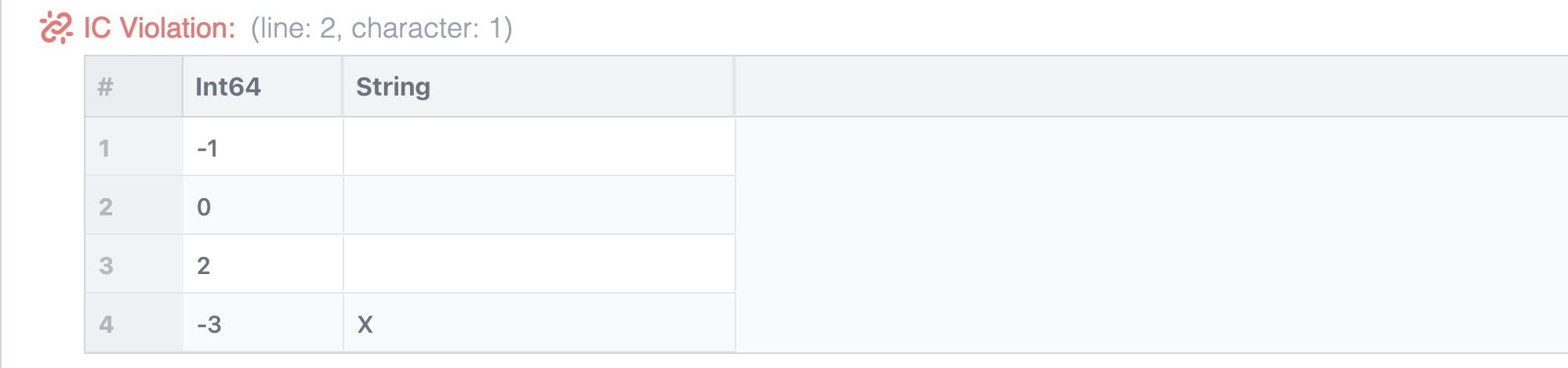

You can express your requirement for both unary and binary relations by providing two bound declarations:

bound R[x in Int] { x >= 0 }
bound R[x in Int] { x >= 0, Any }
 
def R = 2; 0; -1; "a"         // Unary
def R = (-3, "X"); (3, "Y")   // Binary
def R = ("Y", -1, 5.0)        // Ternary

You will then see only those tuples that are not allowed by any of the bound declarations, but you will see them twice:

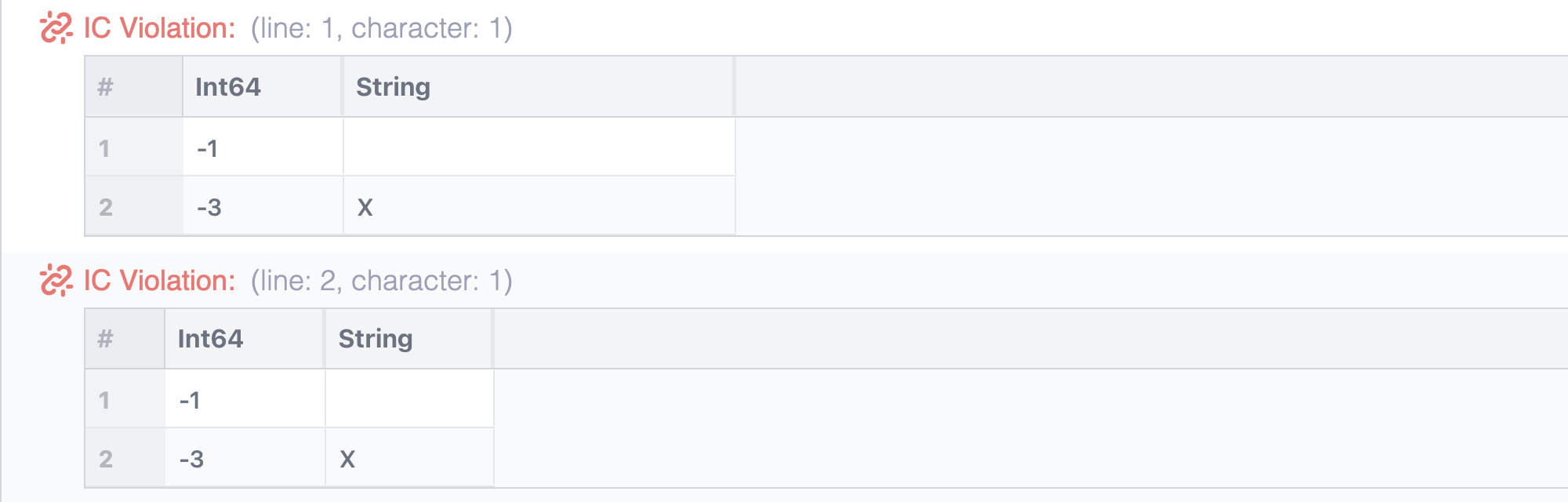
In order to see only one IC violation, you can combine the two bound declarations:

bound R[x in Int] { x >= 0, (true ; Any) }

The factorization above relies on the fact that P, true is equivalent to P, for any relation P.

Finally, you can express this constraint for all relations whose first column is integer. For example:

bound R[x in Int] { x >= 0, y... from y... }
 
def R = 2; 0; -1; "a"         // Unary
def R = (-3, "X"); (3, "Y")   // Binary
def R = ("Y", -1, 5.0)        // Ternary
def R = (0, 1, 2, 3, 4, 5); (-1, 2, 3, 4, 5, 6)

Here is yet another example of the expressiveness of bound declarations. You want to say that any relation whose name is R, whose arity is at least 2, and whose first two columns are integer, should satisfy the following requirements:

• The first element of each tuple is smaller than the second one.
• Each tuple has three elements, and the last element should be a string.

All this is expressed by the following:

bound R[x in Int][y in Int] { x < y, String }

A simple test confirms that the effect is as intended:

bound R[x in Int][y in Int] { String, x < y }
 
def R = (2, 3, "a"); (6, 5, "b")
def R = (7, 8); ("a", 1); (2, "b")

An Extended Example

Consider 10 example definitions of relation R:

1. def R = false.
2. def R = true.
3. def R = 17.
4. def R = "a string".
5. def R = 1, "two".
6. def R = "one", 2.
7. def R = 3, 4.
8. def R = "three", "four".
9. def R = 5, 6, 7.
10. def R = "five", "six", "seven".

In the following table each row shows which of these definitions are allowed by the bound declaration shown at the beginning of the row. The bound declarations are also paraphrased in English in the text that follows the table. Notice that definition 1 is allowed by all bound declarations — the empty set is a subset of any set.

Each of these bound declarations is briefly explained below:

1. bound R = Int
   Relation R must be a subset of Int.

2. bound R(x) = Int(x)
   If relation R is unary, it must be a subset of Int.

3. bound R[x] = Int(x)
   If the arity of relation R is at least 1, then it must be a subset of Int.

4. bound R[x] = Int
   If the arity of relation R is at least 1, then it must be a subset of Any, Int.

5. bound R(x, y) = Int(x)
   If the arity of relation R is 2, then it must be a subset of Int, Any.

6. bound R(x, y) = Int(x), String(y)
   If the arity of relation R is 2, then it must be a subset of Int, String.

7. bound R[x][y] = Int(x), String(y)
   If the arity of relation R is at least 2, then it must be a subset of Int, String.

8. bound R[x](y) = Int(x) and String(y)
   Equivalent to bound declaration 6 above.

9. bound R[x][y] = Int, String
   If the arity of relation R is at least two, then it must be a subset of Any, Any, Int, String.
   For example, def R = "a", "b", 1, "c" would be allowed.

10. bound R[x] = Int(x), String
    If the arity of relation R is at least 1, then it must be a subset of Int, String.

11. bound R = Int, String
    Relation R must be a subset of Int, String.

12. bound R(x, y) = Int(x)
    If the relation R has arity 2, then it must be a subset of Int, Any.

13. bound R[x][y] = Int(x)
    If the arity of relation R is at least 2, then it must be a subset of Int, Any.

14. bound R[x in Int][y] = false
    Does not allow a relation such that its name is R, its arity is at least 2, and the first element of each tuple is an integer.

15. bound R[x in Int][y] = true
    If a relation’s name is R, its arity is at least 2, and the first element of each tuple is an integer, then that relation must be a subset of Int, Any.

Bound Declarations in Modules

Bound declarations are not allowed in parameterized modules that have nonconstant parameters. This is because integrity constraints are not allowed in such modules.

Apart from that, bound declarations are allowed in a module, and apply to relations defined in that module.

For example:

module M
  bound R = Int, Int
  def R = (7, 8); (7, "a"); (7, 8, 9)
  def Q = "something"; "else"
end
def R = (1, "b"); (2, 3, 4)

You can also declare a similar bound from outside the module:

module M
  def R = (7, 8); (7, "a"); (7, 8, 9)
  def Q = "something"; "else"
end
def R = (1, "b"); (2, 3, 4)
 
bound M:R = Int, Int

You can also make sure that a module contains only the relations specified by the bound declarations:

module M
  def R = (7, 8); (7, "a"); (7, 8, 9)
  def Q = "something"; "else"
end
def R = (1, "b"); (2, 3, 4)
 
bound M = :R, Int, Int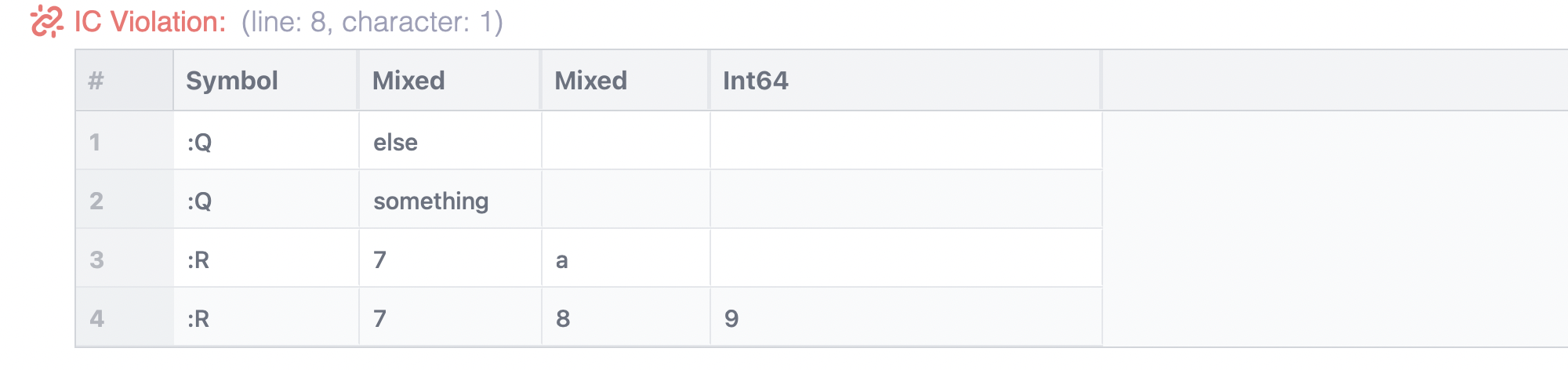

Bound Declarations for Loaded Data

Bound declarations are particularly useful for checking whether all imported data conform to the expected format. When the amount of data is large, finding nonconforming items by visual inspection can be very costly and difficult.

Here’s an example of importing JSON data into a relation:

// read query
 
def config[:data] = """
  {"friends":
    [ {"name": "John", "phone": [{"no.":"1234"}, {"no.":"4567"}]},
      {"name": "Mary", "phone": {"no.":"2468"}}
    ]
  }
"""
def Data = load_json[config]
 
def output = Data

If you write your application with the assumption that each person has a list of phone numbers, then the information for Mary may cause problems, or — worse — be silently ignored. The remedy is to declare a bound declaration that restricts the resulting relation to the expected format:

bound Data =
   :friends, :[], Int, :name, String ;
   :friends, :[], Int, :phone, :[], Int, :"no.", String

It is now almost immediately clear that the line for Mary should be corrected:

      {"name": "Mary", "phone": [{"no.":"2468"}]}

The IC violation will disappear, and the resulting relation will contain tuples of only two kinds:

Next: Value Types