Elements of a Relational Knowledge Graph
This concept guide explains what a relational knowledge graph (RKG) is. It also covers the semantic implication of graph components, demonstrates the steps to build an RKG, and provides examples of how to run simple queries over it.
Introduction
A relational knowledge graph (RKG) is a knowledge graph represented in accordance with the relational data model. This means that an RKG represents each component of a knowledge graph (node, edge, and hyperedge) in the form of relations. You can think of a relational knowledge graph as a relational database composed of multiple relations, which fulfill specific roles.
To make full use of the relational data model, the relational knowledge graph is stored in a fully normalized form and each data point contains semantic meaning. This data modeling strategy is called Graph Normal Form (GNF). See the Graph Normal Form guide for more details.
This guide focuses on the schema and the semantic meaning of each graph component. Understanding these foundations is essential to successfully building a relational knowledge graph that represents your domain of interest.
This guide also illustrates each graph component discussion using object-role modeling (ORM) diagrams. For more details, see Schema Visualization.
Here is an overview of all graph components, their definitions, and how they appear in Rel:
| Graph Component | Definition | Example |
|---|---|---|
| graph | A module of relations containing labeled nodes, edges, and hyperedges. | graph |
| node | A value or identifier representing a concept in the graph. You can reference each node by a unary (arity-1) relation named by a node label. | NodeLabel(node) |
| edge | A pair of nodes in the graph. You can reference each edge by a binary (arity-2) relation named by an edge label. | edge_label(source_node, target_node) |
| hyperedge | A tuple of three or more nodes in the graph. You can reference each hyperedge by a ternary or larger (arity-3+) relation named by a hyperedge label. | hyperedge_label(node_1, node_2, node_3) |
Those familiar with labeled-property graph (LPG) diagrams will recognize two additional graph component names, “node property” and “edge property.” In Rel, these are just special cases of edges and hyperedges respectively.
| LPG Component | Definition | Example |
|---|---|---|
| node property | A value node connected to an entity node via an edge. The edge label is the property name. In a Rel graph, property values are nodes in their own right. | Name(person, “Alice”) |
| edge property | A value connected to two or more nodes via a hyperedge. The hyperedge label is the property name. In a Rel graph, edge property values are nodes in their own right. | employs_since(company, person, 2020) |
Graph
You can define an RKG in Rel in the scope of a single module. Each graph component is represented by a relation, and the module serves as a container encompassing these relations. The names of the relations within this module act as labels that group the graph components into sets of nodes, edges, and hyperedges.
For example, you can declare a module CompanyGraph as follows:
module CompanyGraph
//Define the nodes.
def Person = . . .
//Define the edges.
def employs = . . .
//Define the hyperedges.
def employs_since = . . .
endTo query the data defined in modules, you can either add module_name: before the defined elements, or you can use the with <module> use <relation> syntax.
See Building a Graph for a detailed example of how to populate and query a graph.
Nodes
When expressing your schema in natural language, nodes serve as nouns, each denoting a concrete or conceptual “thing.” In retail, for example, a node can correspond to a physical product. Alternatively, a node may represent an abstract but well-understood concept, such as a customer or supplier.
In some cases, nodes do not translate to “things” at all. Nonetheless, treating these abstractions as nodes is useful for understanding how your data are connected.
Nodes in a relational knowledge graph are either entity nodes or value nodes. Only entity nodes are required to be referenced with labeled node relations. Value nodes are usually used to represent object properties.
As a rule of thumb, entity nodes are represented by graph-unique keys, and value nodes contain human-readable data. See Things Not Strings in Rel for more details on how to represent data using entity and value types.
Entity Nodes
Entity nodes represent people, objects, or concepts.
Defining Entity Nodes
To define an entity node, you need an entity type declaration.
For example, you can declare an entity type Person by specifying the schema of the identifying attributes of a person who is an employee in a company:
entity type Person = String
bound Person = EntityThis specifies that the person’s name (String) identifies them.
Given that once an entity is created it is no longer intrinsically connected to the values that identified it, it is advisable to introduce a bound (opens in a new tab) declaration when defining the schema of an entity node.
For instance, the declaration bound Person = Entity ties Person to the relation Entity.
Every entity type declaration creates an entity constructor relation ^Person(id..., node) that maps the identifiers, id..., to a unique key, node, which will be used to reference the entity node.
You can specify the data types of the identifiers in the entity type declaration (see code above).
The leading caret ^ (^Person) indicates that this is a constructor relation.
Populating Entity Nodes
You can use the constructor ^Person to populate the graph with the names of people.
For example:
def Person = {
^Person["Alice Zhao"];
^Person["Bob Yablonsky"];
^Person["Ava Nguyen"]
}The relation Person now contains the nodes keys of the three person nodes.
Here you can use point-free syntax, where the expression ^Person[id...] evaluates to the unique node key.
Typically, Rel graph nodes are uppercase, and multiword labels are linked directly with no spaces (UpperCamelCase).
What Should an Entity Node Represent?
Determining which aspects of your domain should be modeled as an entity is a design decision left to the developer.
Generally speaking, the following concepts are great examples of entity nodes:
- Objects with many properties.
- Abstract concepts that have nontrivial substructures.
- Entities in an Entity Relationship (ER) diagram.
- Primary keys in a relational table.
- Subjects in the RDF triplestore (opens in a new tab).
Value Nodes
Value nodes represent data, like node property values.
Defining Value Nodes
To define a value type, you need to specify the schema.
For example, here’s how to define a new value type Quarter that represents three-month periods:
from ::std::datetime import Date
value type Quarter = Date, DateThe code above defines Quarter by two Date values: a start date and an end date.
Similarly to entity declarations, value type declarations create a constructor relation, ^Quarter(id..., value), which starts with a caret, ^.
The identifying attributes id... map to the value, value, which captures all the information in id... in one value.
For more details, see Value Types.
Populating Value Nodes
Unlike Entity nodes, value nodes do not need to be explicitly defined in the graph. It is sufficient to just link to them when creating the edges of the graph. See Edges for more details on how to ensure that nodes have the appropriate value type.
You can model value nodes similarly to entity nodes, by defining the relation Quarter:
def Quarter = {
^Quarter[2022-01-01, 2022-03-31];
^Quarter[2022-04-01, 2022-06-30]
}Here again, you can use the relation ^Quarter to populate the node.
The name of the value node doesn’t need to match the name of the underlying value type, but it is conventional to do so. For instance:
def FiscalQuarter = {
(^Quarter[2022-01-01, 2022-03-31])
}This value node declaration is also valid.
What Should a Value Node Represent?
As with entities, determining what should be modeled as a value node is a design decision left to the developer.
Generally speaking, the following concepts are great examples of value nodes:
- Properties of an object.
- Attributes of an entity in an ER diagram.
- Columns of a relational table that are not primary or foreign keys.
- Objects in the RDF triplestore (opens in a new tab).
- Concepts with very few properties.
Edges
If nodes denote “things” in your graph, edges describe the relationships between those things. They correspond to the verbs that connect your nouns. Edges can connect entity nodes to each other, as well as to value nodes. They can even connect value nodes to one another.
Edges Between Entity Nodes
To add an edge between two entity nodes, you need to add a relation to your graph.
In the Company example, you can define the edge employs between the entity nodes Person and Company, and populate it with the node identifiers ^Person and ^Company:
def employs = {
(^Company["RAI"], ^Person["Ava Nguyen"]);
(^Company["RAI"], ^Person["Alice Zhao"]);
(^Company["Microsoft"], ^Person["Alice Zhao"]);
(^Company["Microsoft"], ^Person["Bob Yablonsky"]);
}Typically, Rel graph edges are lowercase, and multiword labels are linked with underscores _ (snake_case).
You can also use Strings as edge names, for example, :"employed by".
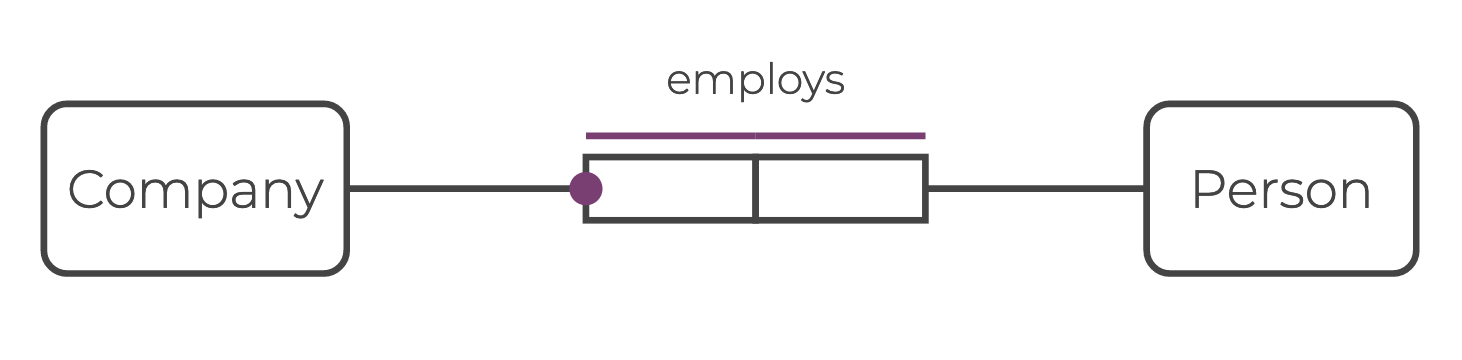
Edge definitions are inherently directional, from source to target.
To change a binary edge into an undirected one, you need to make the underlying relation symmetric.
You can do this using transpose:
def spouse = transpose[spouse]Node Properties
Adding an entity node property is equivalent to connecting an entity and a value node via an edge. The process is similar to connecting two entity nodes. However, in this case, the target node of the edge doesn’t contain an entity node identifier; it instead contains the property value itself.
Here’s how to populate the property born_on for each Person node:
def born_on = {
(^Person["Alice Zhao"], 1982-03-15);
(^Person["Bob Yablonsky"], 1991-11-22);
(^Person["Ava Nguyen"], 1979-09-09)
}For property values, you can safely omit writing a value type declaration as long as you give the data a unique property name. Value nodes are leaf nodes in the graph.
If the node property has a value type, add the edge just as you would an edge between two entity nodes.
For example, you can declare a value type String for the node property Name as follows:
value type Name = StringThen you can add a ^Name node property to each entity node ^Person as follows:
def has_name = {
(^Person["Alice Zhao"], ^Name ["Alice Grace Zhao"]);
(^Person["Bob Yablonsky"], ^Name ["Bob Matthew Yablonsky"]);
(^Person["Ava Nguyen"], ^Name ["Ava Marie Nguyen"])
}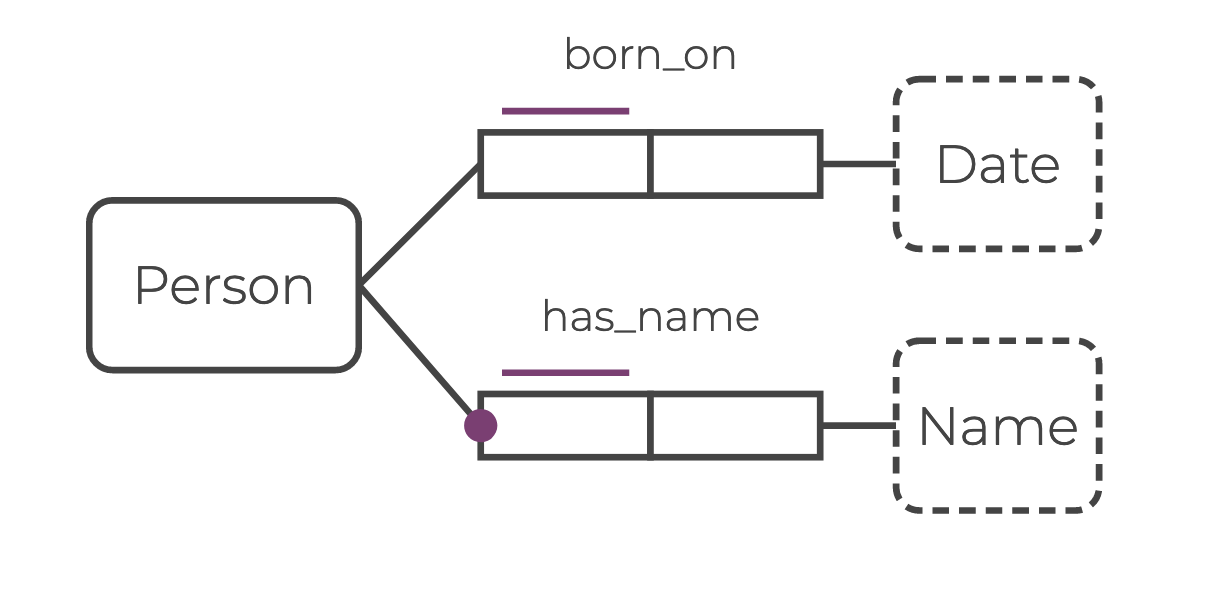
The purple bar in the ORM diagram above indicates a uniqueness constraint.
Here the purple bar above the edge has_name means “each Person has at most one Name.”
The purple dot indicates a mandatory role constraint.
In this case it means “each Person has at least one Name.”
Combining the constraints means “each Person has exactly one Name.”
Edges Between Value Nodes
For most applications, source nodes are entity nodes.
However, in some circumstances, you may want to connect value nodes together.
For example, say you want to add an edge between the two value types Date and Year:
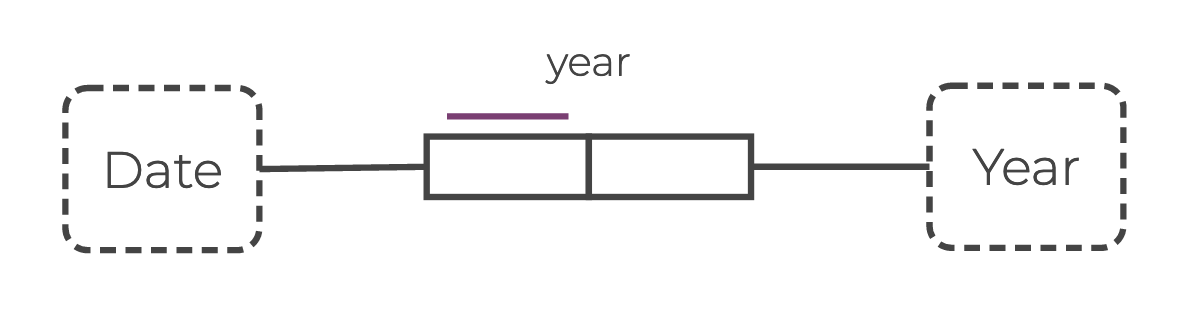
In Rel, you can define this edge as follows:
def year(date, year) {
^Date(year, _, _,date)
}In the Company example, you can connect the properties of dates like this:
def start_month(quarter_node, month) {
(^Quarter[start_date, _, quarter_node], date_month[start_date, month])
from start_date
}Hyperedges
A hyperedge connects three or more nodes — usually multiple entity nodes — to each other. However, it’s also possible for a hyperedge to connect entity nodes to value nodes.
Hyperedges are relations with composite keys that are made up of two or more individual keys. Hyperedge relations — like all relations — may or may not have a value column. If they do, each composite key points to only one value, which is located in the last column in the relation. If the hyperedge relation describes a boolean-like relationship — one that is either true or false — the relation only stores the composite key and does not have a value column.
One common use case for hyperedges is to store higher dimensional data like embeddings.
Edge Properties
Just as nodes can have properties, so can edges. Edge properties are represented in Rel using hyperedges.
In natural language, if the source node corresponds to the subject and the target node to the direct object, an edge property serves as the indirect object. You can express edge properties as objects of prepositions, like “since,” “on,” “for,” “by,” etc.
In Rel, an edge property is a value node connected to two or more entity nodes via a ternary edge.
For example, ”RelationalAI has employed Alice since 2020.” You can infer that:
- A binary edge
employsconnects theCompanyentity node for “RelationalAI” and thePersonentity node for “Alice.” - The ternary edge (hyperedge)
employs_sinceconnects the “RelationalAI” and “Alice” entity nodes to a value nodeYear, with the value2020. The value node is the edge property.
Here is an ORM diagram for this relationship. Note that you can read the ORM diagram just like a sentence across the set of role boxes: ”Company employs Person since Date.”
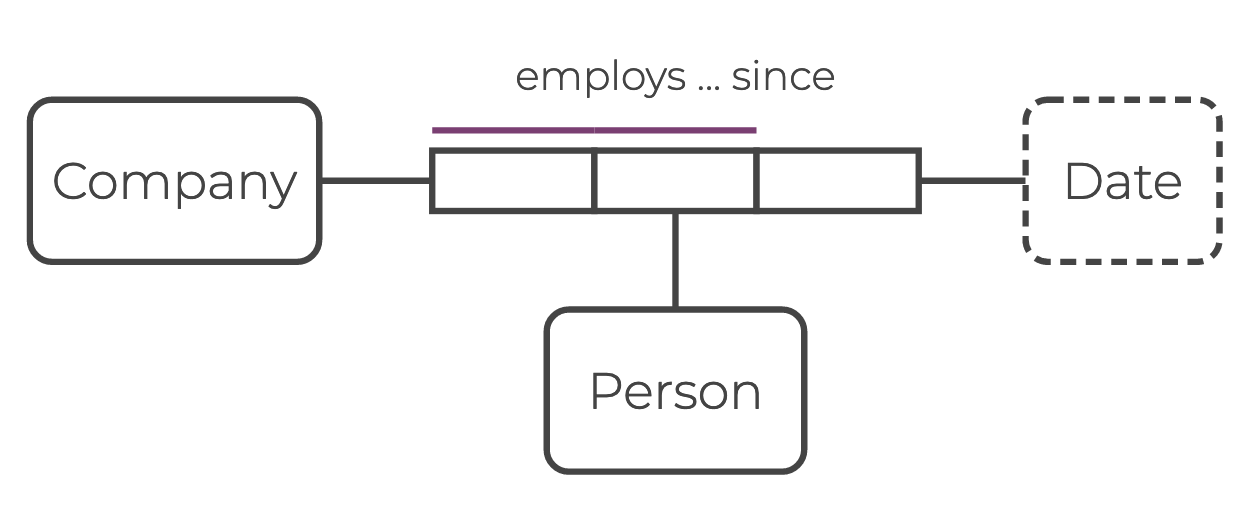
Defining Edge Properties
You can define hyperedges similarly to binary edges.
For example, you can define the edge property employs_since in the diagram above as:
def employs_since = {
(^Company["RAI"], ^Person["Ava Nguyen"], 2019-12-01);
(^Company["RAI"], ^Person["Alice Zhao"], 2020-05-10);
(^Company["Microsoft"], ^Person["Alice Zhao"],2021-08-24);
(^Company["Microsoft"], ^Person["Bob Yablonsky"], 2018-02-28)
}What Should an Edge Property Represent?
Edge properties can represent a range of information about the graph. They often reflect a condition or degree under which the edge is valid.
The following are good examples of edge properties:
- Reliability (as a weight).
- Information source.
- Time or location.
- Time- or location-dependent datum, as a quaternary (arity-4) hyperedge.
Optional and Incomplete Data
Note that the hyperedge example employs_since only connects entities for which there is a value for the edge property.
If there is no property value for a particular edge, this relation does not exist.
Here, the employs edge connects the nodes, and this is the sort of graph connectivity you want to represent in most cases.
However, if it is important to show in the schema that the edge property is missing, you can use Rel’s Missing type.
Hyperedges of Any Size
Edge properties are just one subset of hyperedges. Rel is agnostic to the dimension of a hyperedge or to the combination of entity and value nodes that the hyperedge contains.
Consider the following example fact: ”Alice met Bob at the Strange Loop conference in 2021.”
This can be modeled as an arity-4 hyperedge met_at_place_in_year:
def met_at_place_in_year(person1, person2, conference, year) {
person1 = ^Person["Alice Zhao"],
person2 = ^Person["Bob Yablonsky"],
conference = ^Conference["Strange Loop"],
year = 2021
}Reification
While Rel supports hypergraphs of any dimension, graph traversal algorithms are optimized for binary graphs. Reification is a process by which you can transform hyperedges into binary relationships. Reifying a hyperedge is a two-step process:
-
Define a new reified entity using the key of the hyperedge relation (every node but the last, target node):
def ^ReifiedEntity {(String, std::datetime::Date}def ReifiedEntity(e): exists((s, d) | e = ^ReifiedEntity[s, d] and a_hyperedge(s, d, _) ) -
Connect a new labeled edge
reified_edgefrom the new reified entityReifiedEntityto the target nodet:def reified_edge(source_node, target_node): exists((s, d) | source_node = ^ReifiedEntity[s, d], target_node = a_hyperedge[s, d] )
You can also define new labeled edges to connect them to each node in the hyperedge key. For example, say you want to reify the example ”Company employs Person since Date” represented below.

Here are the steps you need to follow:
-
Define and populate a new node (
Employment) that captures the relationship ”Company employs Person“:entity type Employment = String, Stringdef Employment(employment) { exists(company, person : employment = ^Employment[company, person] and employment_since(company, person, _) ) } -
Connect the reified
Employmentnode to each node (Company,Person, andDate) of theemploys_sincehyperedge. This requires defining three new labeled edges:has_employer,has_employee, andemployment_since. For example:def has_employer(employment, company) { exists(person: employment = ^Employment[company, person] and employment_since(company, person, _) ) } def has_employee(employment, person) { exists(company: employment = ^Employment[company, person] and employment_since(company, person, _) ) } def employment_since(employment, dt) { exists(company, person: employment = ^Employment[company, person] and employment_since(company, person, dt) ) }
Here’s the ORM diagram representation of the reification:
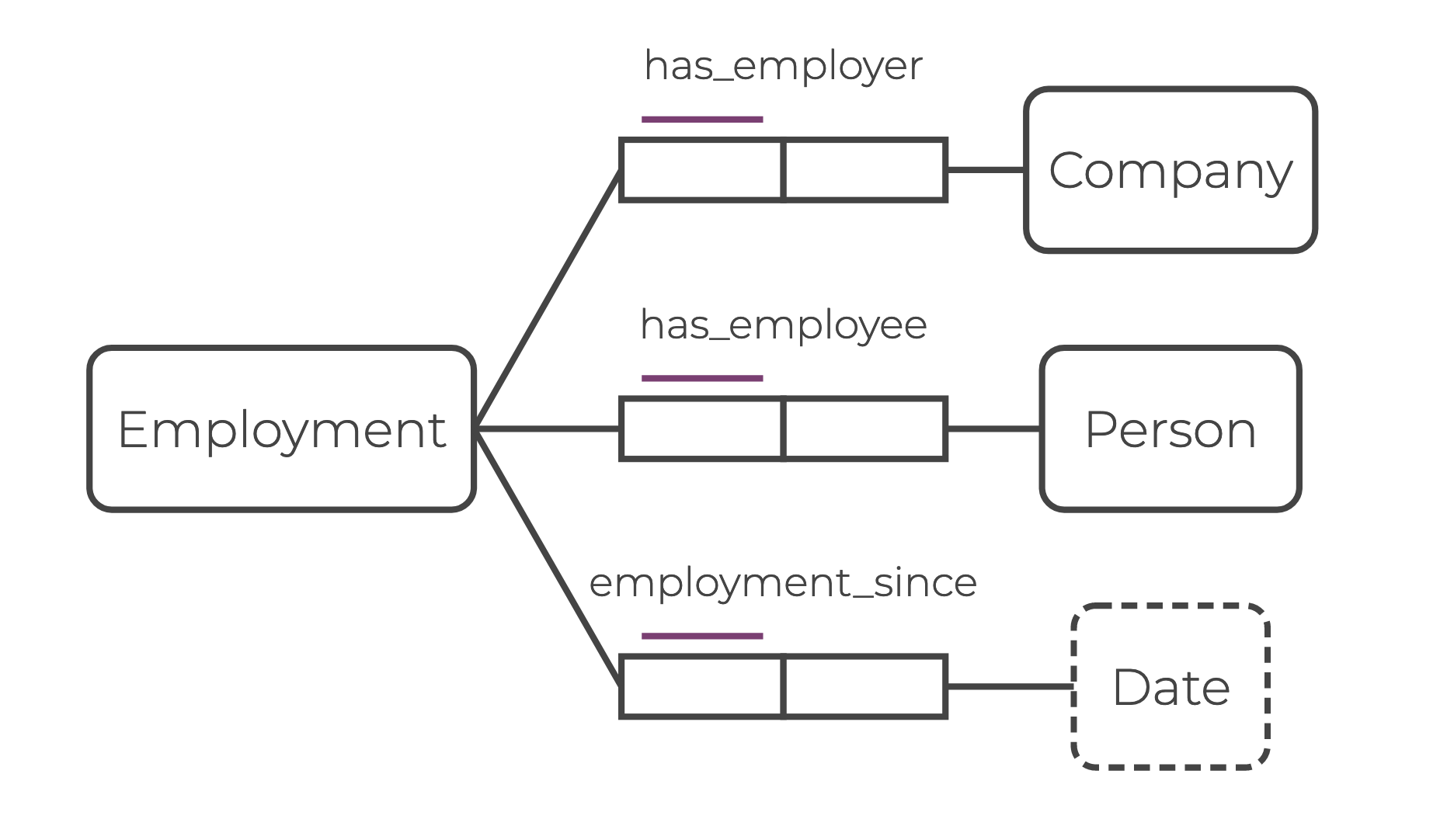
The new edges has_employer, has_employee, and employment_since are all binary.
The entity node label Employment may not be obvious in the source data, but the construction of hyperedges can point to natural places where new concepts, and new node labels, can be generated.
Embeddings
You can store structural and semantic information in hyperedges through embeddings. Embeddings represent concepts or words in a numerical format, typically as vectors. This allows graph algorithms and machine learning models to operate over these concepts. Vectors, matrices, or any tensors can be represented as relations with arity 2, 3, or , respectively, where is the rank of the tensor.
The schema of the underlying relation — representing the embedding — is (key_graph..., key_tensor..., value).
The graph-related key key_graph... identifies the node or edge associated with the embedding.
The tensor indices are captured by key_tensor....
Together they make up the composite key of the relation.
Note that both keys may be composite keys themselves, which is indicated by ....
It’s good practice to store embeddings in a separate module, rather than as hyperedges. A single graph may have many sets of embeddings associated with it.
The following example initializes a 10-dimensional vector embedding for the Person entity with zeros:
def mygraph_embedding:Person(person, dimension, value) {
person = mygraph:Person,
dimension = range[1, 10, 1],
value = 0.0
}Here, the graph-related key is the entity ID person and the tensor index is dimension.
Similarly, you can define a 10x10 matrix embedding for an edge with uniformly distributed random values between 0 and 1 using the Threefry pseudorandom number generator random_threefry_float64:
def mygraph_embedding:employed_by(person, company, index1, index2, value) {
mygraph:employed_by(person, company),
index1 = range[1, 10, 1],
index2 = range[1, 10, 1],
value = random_threefry_float64[index1, index2]
}In the code above, both the graph-related key (person, company) and the matrix indices (index1, index2) are composite keys.
Using this modeling approach provides great flexibility. You can realize any kind of embedding, ranging from a single value, vector, or matrix to an abstract tensor. Thanks to the high similarities between GNF and sparse matrix representations, embeddings in Rel are stored in the sparse COO (opens in a new tab) format and don’t have to be dense.
Example
Building a Graph
Now that you’re familiar with the elements of a relational knowledge graph, you can start building and querying a simple graph. Here’s an ORM diagram of the knowledge graph you are about to build:
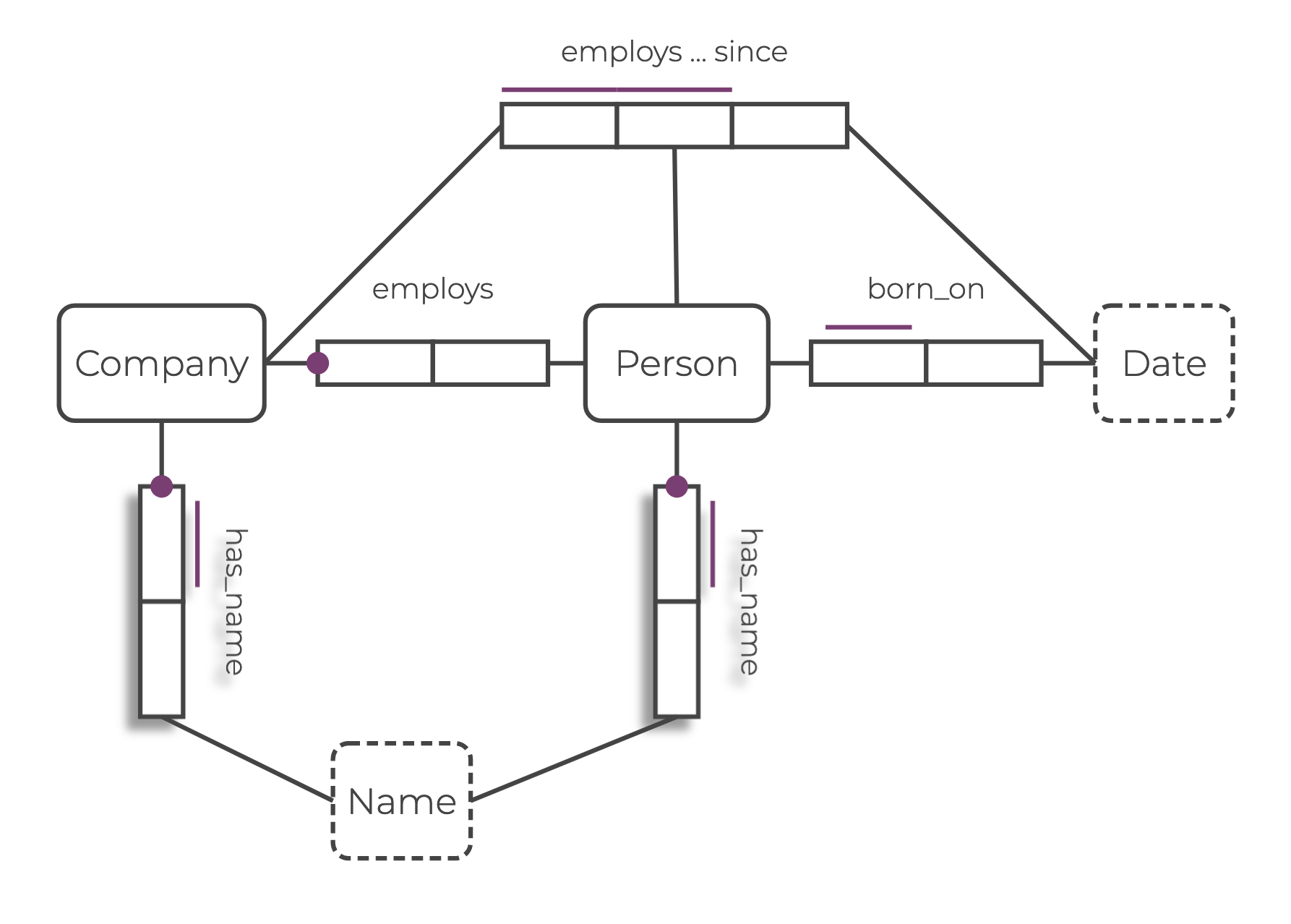
Defining the Schema
The first step is to define the schema.
To do so, start by creating a module called CompanyGraph, which contains relations that represent each graph component.
This guide focuses only on defining the data types of the value and entity nodes.
For a more extensive example defining the data schema of the edges and the expression of semantic constraints, see Graph Schema.
// model
module CompanyGraph
// Entity nodes
entity type Company = String
bound Company = Entity
entity type Person = String
bound Person = Entity
// Value nodes
value type Name = String
endFor more details on the bound syntax, see Bound Declarations in the Rel Reference manual.
Populating the Graph
Now that you have defined the schema, it’s time to insert some data into your database.
As previously mentioned, modules allow you to organize data and group information. So when building a knowledge graph, it makes sense to insert all the data into a module representing the knowledge graph.
Updating the data within a module involves two steps:
- Defining the data within a temporary module (
company_graph). - Storing the data in a base relation (
CompanyGraph), which persists in the database.
// write query
with CompanyGraph use ^Company, ^Person, ^Name
// Define the data within a temporary `company_graph` module.
module company_graph
// Entity node: `Company`
def Company = {
^Company["RAI"];
^Company["Microsoft"]
}
// Entity node: `Person`
def Person = {
^Person["Alice Zhao"];
^Person["Bob Yablonsky"];
^Person["Ava Nguyen"]
}
// Edge: `has_name`
def has_name = {
(^Company["RAI"], ^Name["RelationalAI"]);
(^Company["Microsoft"], ^Name["Microsoft Corporation"]);
(^Person["Alice Zhao"], ^Name ["Alice Grace Zhao"]);
(^Person["Bob Yablonsky"], ^Name ["Bob Matthew Yablonsky"]);
(^Person["Ava Nguyen"], ^Name ["Ava Marie Nguyen"])
}
// Edge: `born_on`
def born_on = {
(^Person["Alice Zhao"], 1982-03-15);
(^Person["Bob Yablonsky"], 1991-11-22);
(^Person["Ava Nguyen"], 1979-09-09)
}
// Edge: `employs`
def employs = {
(^Company["RAI"], ^Person["Ava Nguyen"]);
(^Company["RAI"], ^Person["Alice Zhao"]);
(^Company["Microsoft"], ^Person["Alice Zhao"]);
(^Company["Microsoft"], ^Person["Bob Yablonsky"]);
}
// Hyperedge: `employs_since`
def employs_since = {
(^Company["RAI"], ^Person["Ava Nguyen"], 2019-12-01);
(^Company["RAI"], ^Person["Alice Zhao"], 2020-05-10);
(^Company["Microsoft"], ^Person["Alice Zhao"],2021-08-24);
(^Company["Microsoft"], ^Person["Bob Yablonsky"], 2018-02-28)
}
end
// Store the data in the `CompanyGraph` base relation.
def insert:CompanyGraph = company_graph
This query, and those that follow, begin with a with <module> use <relation> statement.
This allows you to retrieve the information stored in the module.
In this case, the module is CompanyGraph and the relations used are the ones required to define ^Company, ^Person, and ^Name.
Entity and value type declarations automatically create constructor relations, which start with a caret ^.
For more details on the code above, see My First Knowledge Graph.
Querying a Graph
Querying a relational knowledge graph allows you to find specific entities. The following examples show how to write a query based on attributes, an aggregation query, and a query with conditions.
Attribute Query Example
To find specific attributes of entities stored in a relational knowledge graph, you need to write an attribute query.
For example, say you want to answer this question: What company does Alice Zhao work for?
You can write the query below:
// read query
with CompanyGraph use employs, ^Person, has_name
def output(company_name) = {
exists(company :
employs(company, ^Person["Alice Zhao"])
and has_name(company, company_name)
)
}The def output statement in the () specifies what elements are displayed in the output.
In this case, it’s one value: the name of the company fulfilling the statement on the right-hand side of the equal sign.
You can verbalize the right-hand side of the definition as “there exists a company such that the company employs Alice Zhao and the company has a name.”
The code and has_name(company, company_name) connects the entity hash with the entity name, making the output more readable.
Aggregation Query Example
To find data from multiple related tables in a relational knowledge graph, you need to use an aggregation query. This involves using operations like counting, adding, or grouping data to generate aggregated results.
For exmaple, say you want to answer this question: How many employees work at each company?
You can write the query below:
// read query
with CompanyGraph use employs, has_name
def output(company_name, head_count) {
exists(company :
head_count = count[employs[company]]
and company_name = has_name[company]
)
}This query uses the count relation.
The output displays two values: the name of the company and its headcount.
You can express the right-hand side of the definition as “there exists a company such that the company has a name and the headcount is the number of employs edges for that company.”
Conditional Query Example
To find data in a relational knowledge graph based on specified conditions or criteria, you need to use a conditional query.
For example, say you want to answer this question: Who was hired at RelationalAI after 2020?
You can write the query below:
// read query
from ::std::datetime import Date
with CompanyGraph use Name, Company, Person, employs_since, has_name, ^Name
def RAI_hires_after_2020(person_name in Name, dt in Date) {
exists(company in Company, person in Person :
employs_since(company, person, dt)
and has_name(company, ^Name["RelationalAI"])
and dt > 2019-12-31
and has_name(person, person_name)
)
}
def output = RAI_hires_after_2020The statement def RAI_hires_after_2020(person_name in Name, dt in Date) indicates that the definition RAI_hires_after_2020 has a pair of values, person_name and dt, where person_name is of property node Name and dt is of property node Date.
You can verbalize the right-hand side of the definition as “there exists a company and a person such that a company employs a person since a date, the name of the company is RAI, the start date is after 2019-12-31, and the person has a name.”
Summary
A relational knowledge graph represents each component of a knowledge graph (nodes, edges, and hyperedges) in the form of relations. Nodes, which are either entity nodes or value nodes, represent physical and abstract concepts. Edges connect these nodes and describe the relationships between them. Hyperedges, which have edge properties, connect multiple nodes together and add further meaning.
When you define the relations corresponding to each component within modules and store the data populating them in base relations, you create a graph. You can then query this graph to retrieve data based on specific attributes, aggregations, and conditions.
By understanding the semantic meaning of each component and following the step-by-step example in this guide, you can build relational knowledge graphs to model your data.
See Also
To create your first knowledge graph using Rel, see My First Knowledge Graph. For a more complex example, see The Lehigh University Benchmark.